Programming/Kdb/Labs/Exploratory data analysis

Getting hold of data

In this lab we'll make sense of the following data set from the UCI Machine Learning Repository:

• Name: Real estate valuation data set
• Data Set Characteristics: Multivariate
• Attribute Characteristics: Integer, Real
• Associated Tasks: Regression
• Number of Instances: 414
• Number of Attributes: 7
• Missing Values? N/A
• Area: Business
• Date Donated: 2018.08.18
• Number of Web Hits: 111,613
• Original Owner and Donor: Prof. I-Cheng Yeh, Department of Civil Engineering, Tamkang University, Taiwan
• Relevant papers:
  • Yeh, I.C., and Hsu, T.K. (2018). Building real estate valuation models with comparative approach through case-based reasoning. Applied Soft Computing, 65, 260-271.

• URL: https://archive.ics.uci.edu/ml/datasets/Real+estate+valuation+data+set

There are many data sets on UCI that are worth exploring. We picked this one because it is relatively straightforward and clean.

Let's read the data set information:

The market historical data set of real estate valuation is collected from Sindian Dist., New Taipei City, Taiwan. The real estate valuation is a regression problem. The data set was randomly split into the training data set (2/3 samples) and the testing data set (1/3 samples).

This paragraph describes how the original researchers split up the data set. We will split it up differently: fifty-fifty.

Let's read on:

The inputs are as follows:

• X1 = the transaction date (for example, 2013.25=2013 March, 2013.500=2013 June, etc.)
• X2 = the house age (unit: year)
• X3 = the distance to the nearest MRT station (unit: metre)
• X4 = the number of convenience stores in the living circle on foot (integer)
• X5 = the geographic coordinate, latitude (unit: degree)
• X6 = the geographic coordinate, longitude (unit: degree)

The output is as follows:

• Y = house price per unit area (10000 New Taiwan Dollar/Ping, where Ping is a local unit, 1 Ping = 3.3 square metres)

Downloading the data set and converting it to CSV

The data set can be downloaded from the data folder https://archive.ics.uci.edu/ml/machine-learning-databases/00477/. The data is supplied in the form of an excel file, Real estate valuation data set.xlsx. In order to export this data to kdb+/q, we convert it to the comma-separated values (CSV) format:

• start Excel;
• File > Open the file Real estate valuation data set.xlsx;
• File > Save As, set "Save as type" to "CSV (Comma delimited)", click "Save".

Opening the data set in kdb+/q

We read in the resulting CSV file as a kdb+/q table:

t:("HFFFHFFF";enlist",")0:`$":S:/dev/bodleian/teaching/kdb-q/Real estate valuation data set.csv"

(Here you need to replace our path with the corresponding path on your machine.)

We have specified the type for each column as "HFFFHFFF". Here "H" stands for short and "F" stands for float.

We can examine the meta data for the resulting table with

meta t

The result:

c                                     | t f a
--------------------------------------| -----
No                                    | h
X1 transaction date                   | f
X2 house age                          | f
X3 distance to the nearest MRT station| f
X4 number of convenience stores       | h
X5 latitude                           | f
X6 longitude                          | f
Y house price of unit area            | f

It's somewhat inconvenient to work in q with table column names containing spaces, so we rename the columns as follows:

t:`no`transaction_date`house_age`distance_to_nearest_mrt`number_of_convenience_stores`latitude`longitude`house_price_per_unit_area xcol t

We check the meta data again:

meta t

The result:

c                           | t f a
----------------------------| -----
no                          | h
transaction_date            | f
house_age                   | f
distance_to_nearest_mrt     | f
number_of_convenience_stores| h
latitude                    | f
longitude                   | f
house_price_per_unit_area   | f

Producing the time series plot of house_price_per_unit_area

We look at the first 10 rows

select[10] from t

no transaction_date house_age distance_to_nearest_mrt number_of_convenience_s..
-----------------------------------------------------------------------------..
1  2012.917         32        84.87882                10                     ..
2  2012.917         19.5      306.5947                9                      ..
3  2013.583         13.3      561.9845                5                      ..
4  2013.5           13.3      561.9845                5                      ..
5  2012.833         5         390.5684                5                      ..
6  2012.667         7.1       2175.03                 3                      ..
7  2012.667         34.5      623.4731                7                      ..
8  2013.417         20.3      287.6025                6                      ..
9  2013.5           31.7      5512.038                1                      ..
10 2013.417         17.9      1783.18                 3                      ..

and observe that the data is not sorted by transaction_date. We therefore sort it by transaction_date (in-place, hence `t and not t in the following command):

`transaction_date xasc `t

meta t reveals that the data is now sorted by transaction_date:

meta t

c                           | t f a
----------------------------| -----
no                          | h
transaction_date            | f   s
house_age                   | f
distance_to_nearest_mrt     | f
number_of_convenience_stores| h
latitude                    | f
longitude                   | f
house_price_per_unit_area   | f

We see that the transaction_date now has the "sorted" (s) attribute (a).

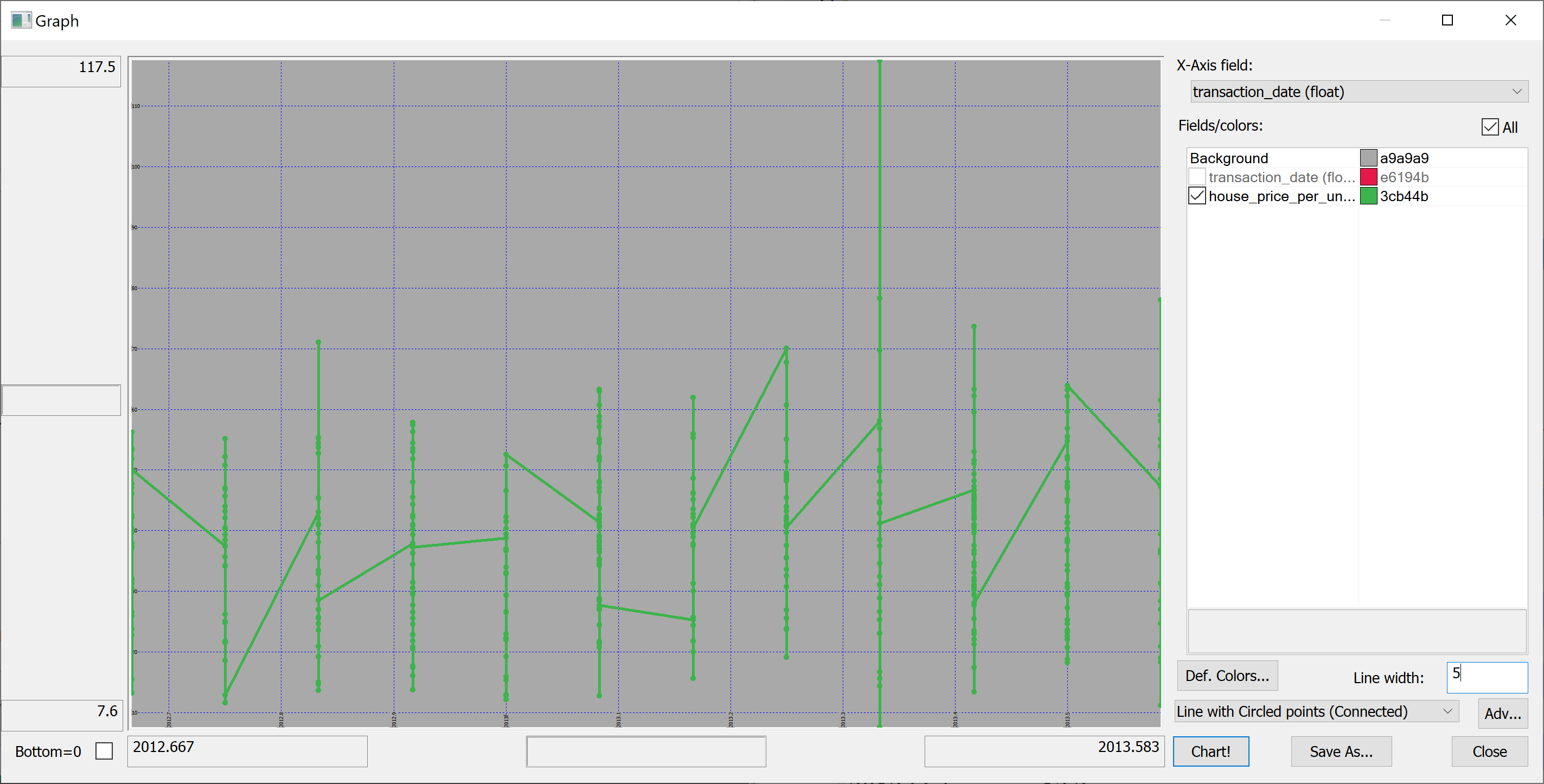
Here is our first attempt to produce a time series plot of house_price_per_unit_area:

select transaction_date, house_price_per_unit_area from t

The resulting plot is confusing because the transaction_date is bucketed into (floating point) months:

(Here we have used Q Insight Pad to plot the results of a q-sql query.)

Can we do better?

Perhaps we could build something on the basis of

select house_price_per_unit_area by transaction_date from t

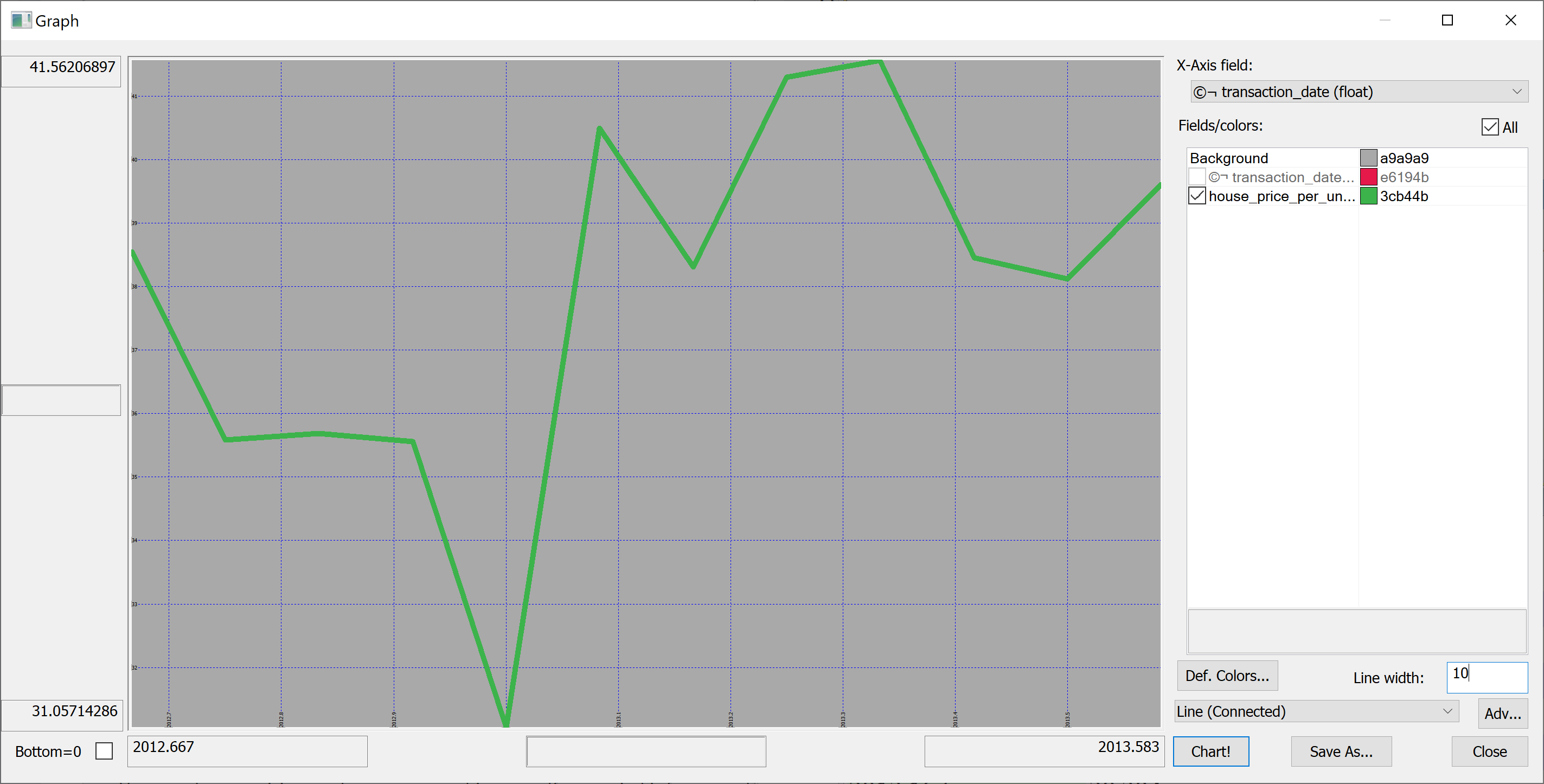
We could produce the plot of the mean house_price_per_unit_area in any given month:

select avg house_price_per_unit_area by transaction_date from t

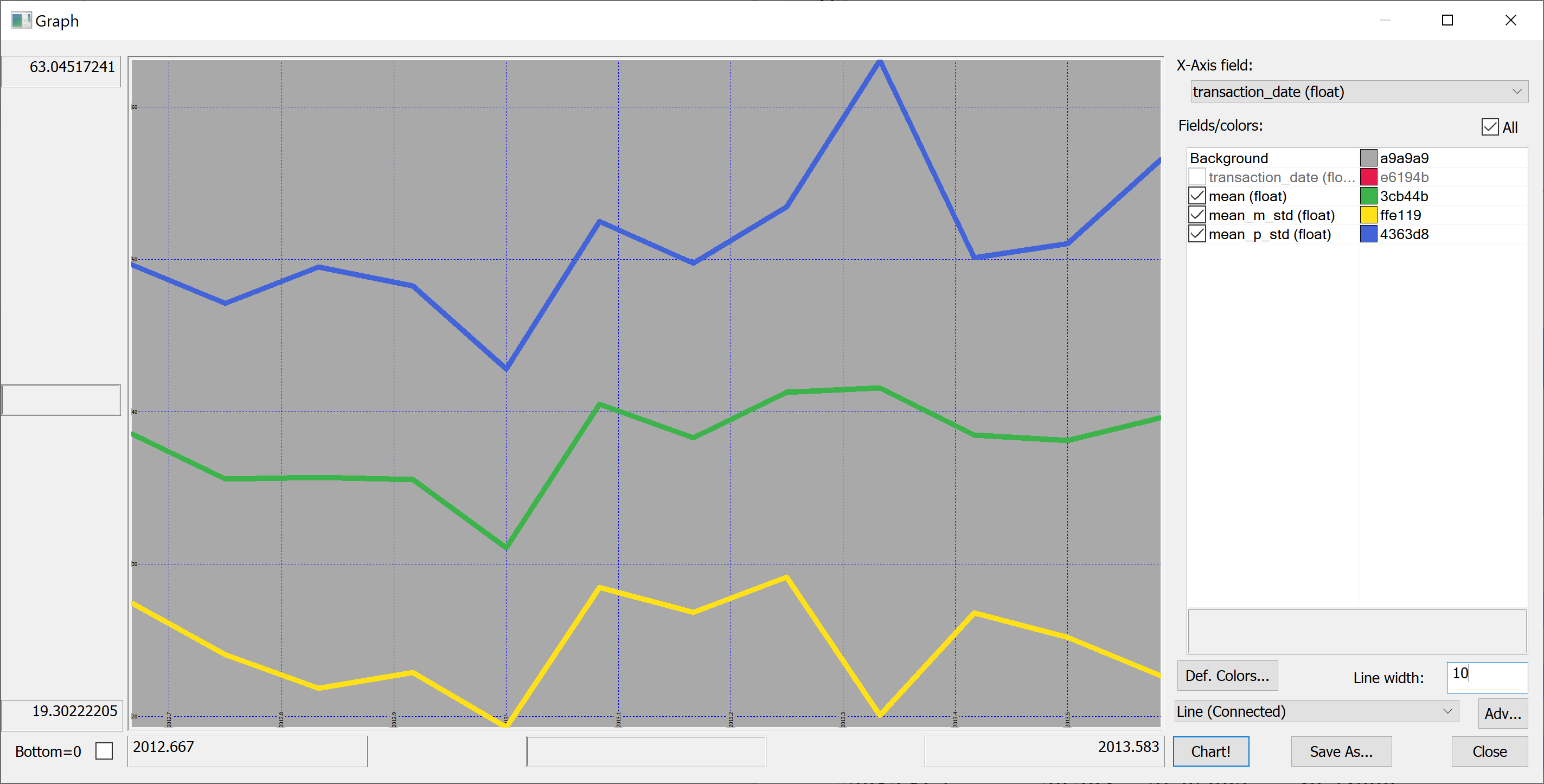
Looking at this plot, it appears that the house prices dropped towards the start of 2013 and then sharply increased again. However, we don't know the uncertainties. We could produce a plot of the mean house prices in any given month +/- one standard deviation:

select transaction_date,mean,mean_m_std:mean-std,mean_p_std:mean+std from
  select mean:avg house_price_per_unit_area,std:sqrt var house_price_per_unit_area by transaction_date from t

Perhaps we shouldn't jump to conclusions regarding the increase / decrease of the house prices over time: the standard deviation is quite high.

Histograms

In order to better understand the data we need to plot some histograms. We define the following function:

getHistogram:{[data;rule]
  / data - array of data
  / rule - function which takes data and returns bins
  bins: rule data;
  update 0^histogram from
    ([bins:asc til count[bins]] x:bins) uj
    (select histogram: count bins by bins from ([] bins:bins binr data))};

This function takes as a parameter a rule — a function that takes the data and returns the bins. We'll use a very simple rule:

histBin:{[n;data]
    / n - number of bins
    / data - array of data
    min[data]+((max[data]-min[data])%n)*til 1+n};

More advanced rules can be found in the library quantQ: https://github.com/hanssmail/quantQ

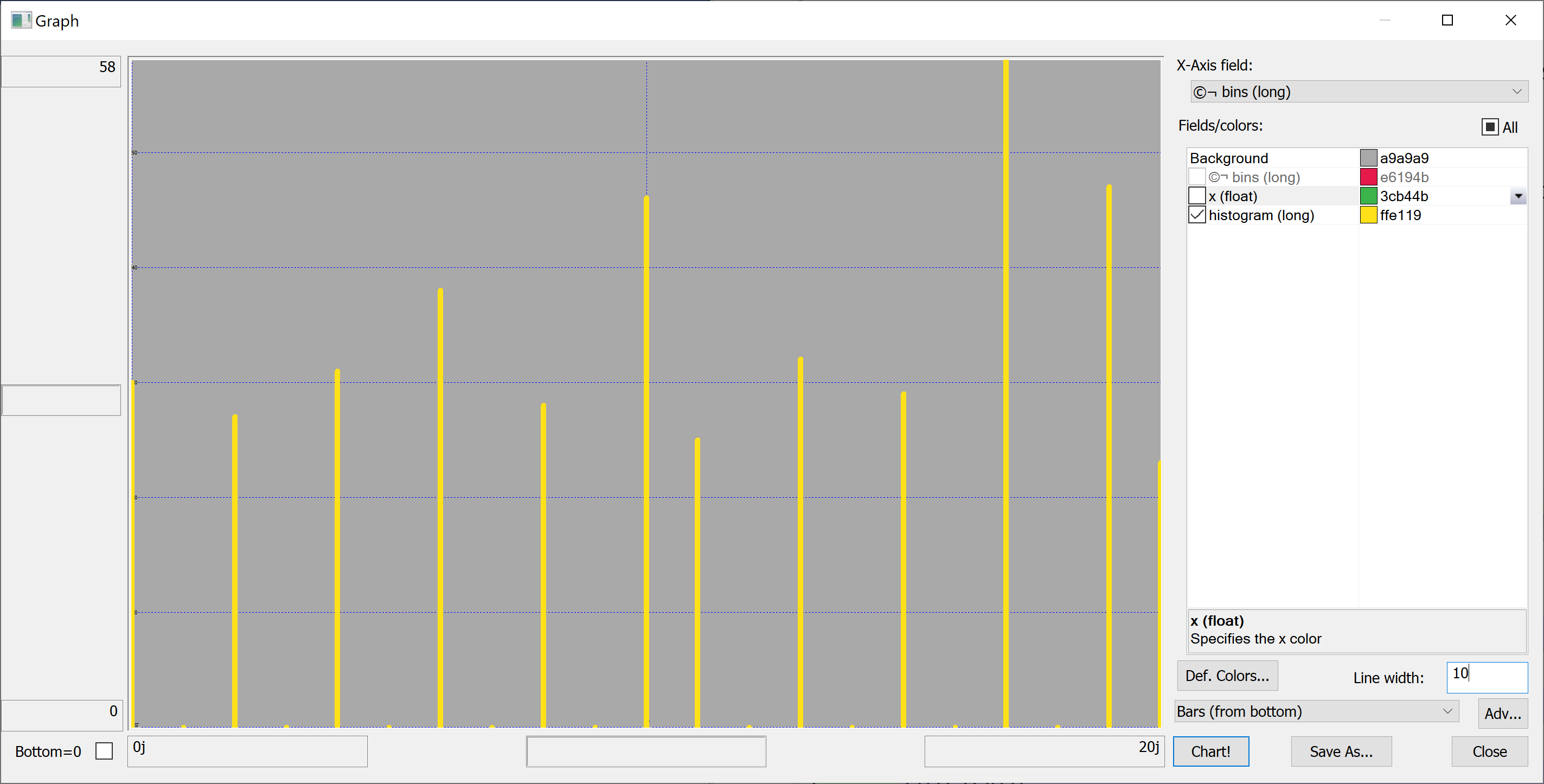
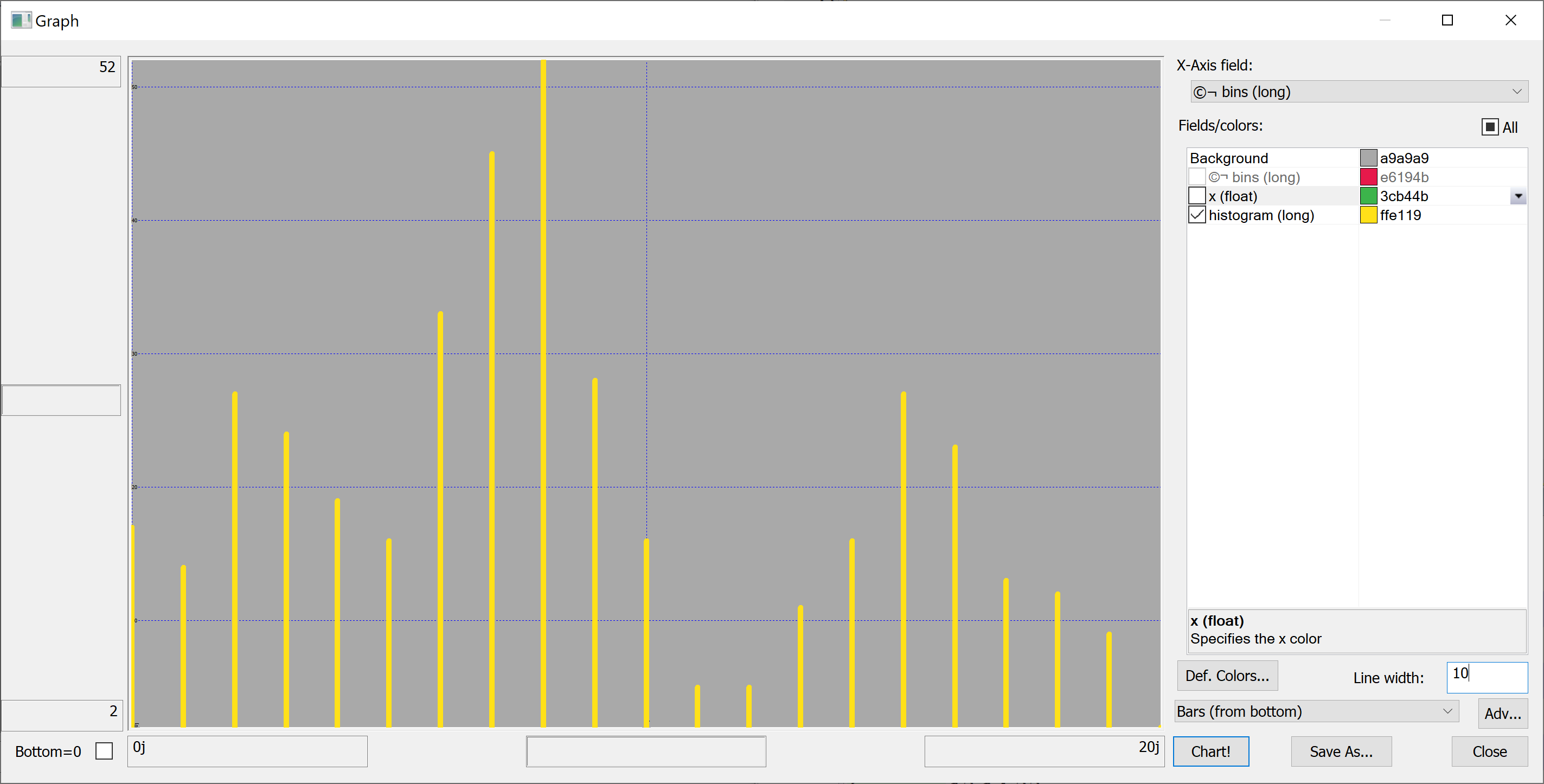
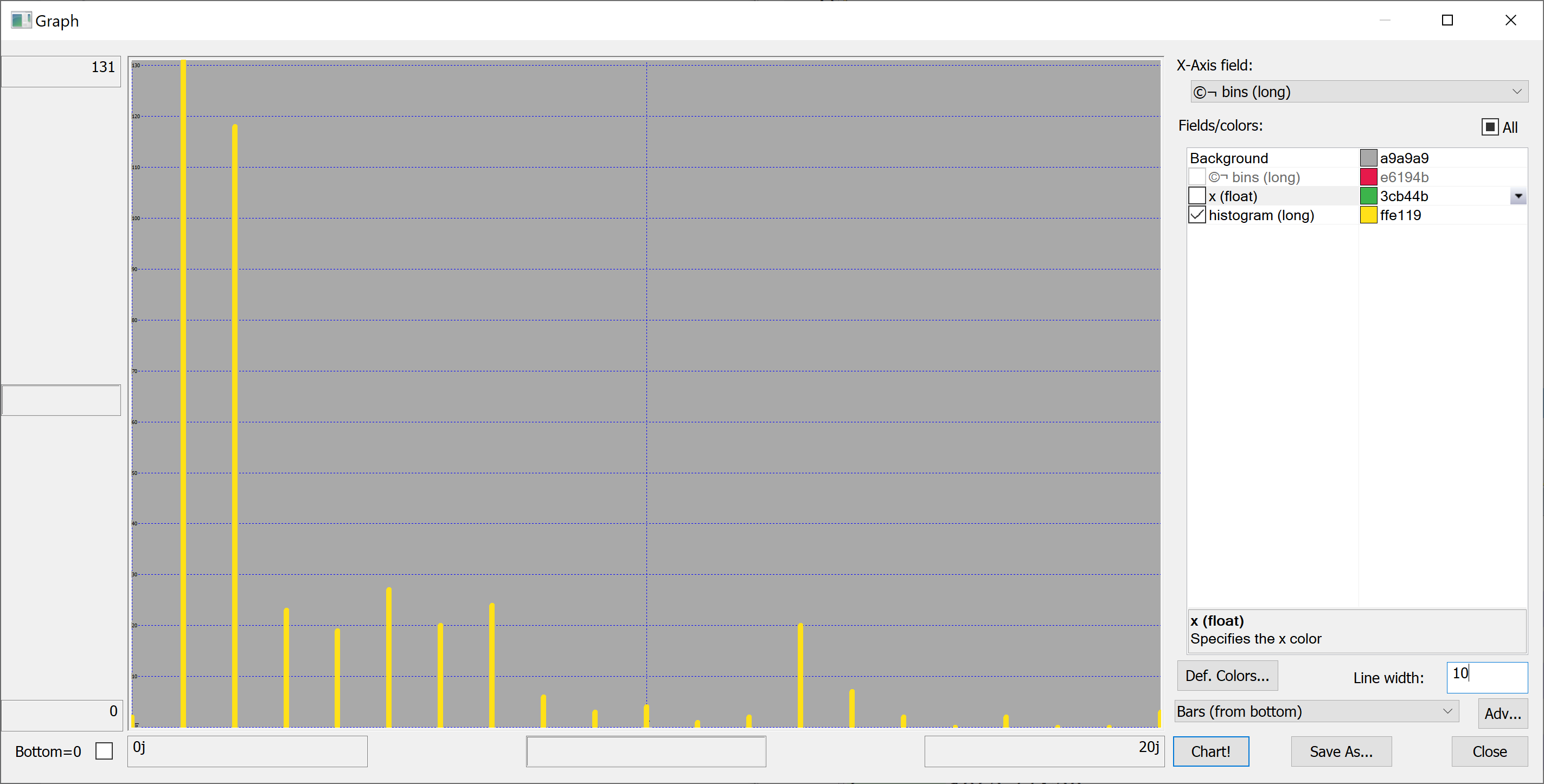
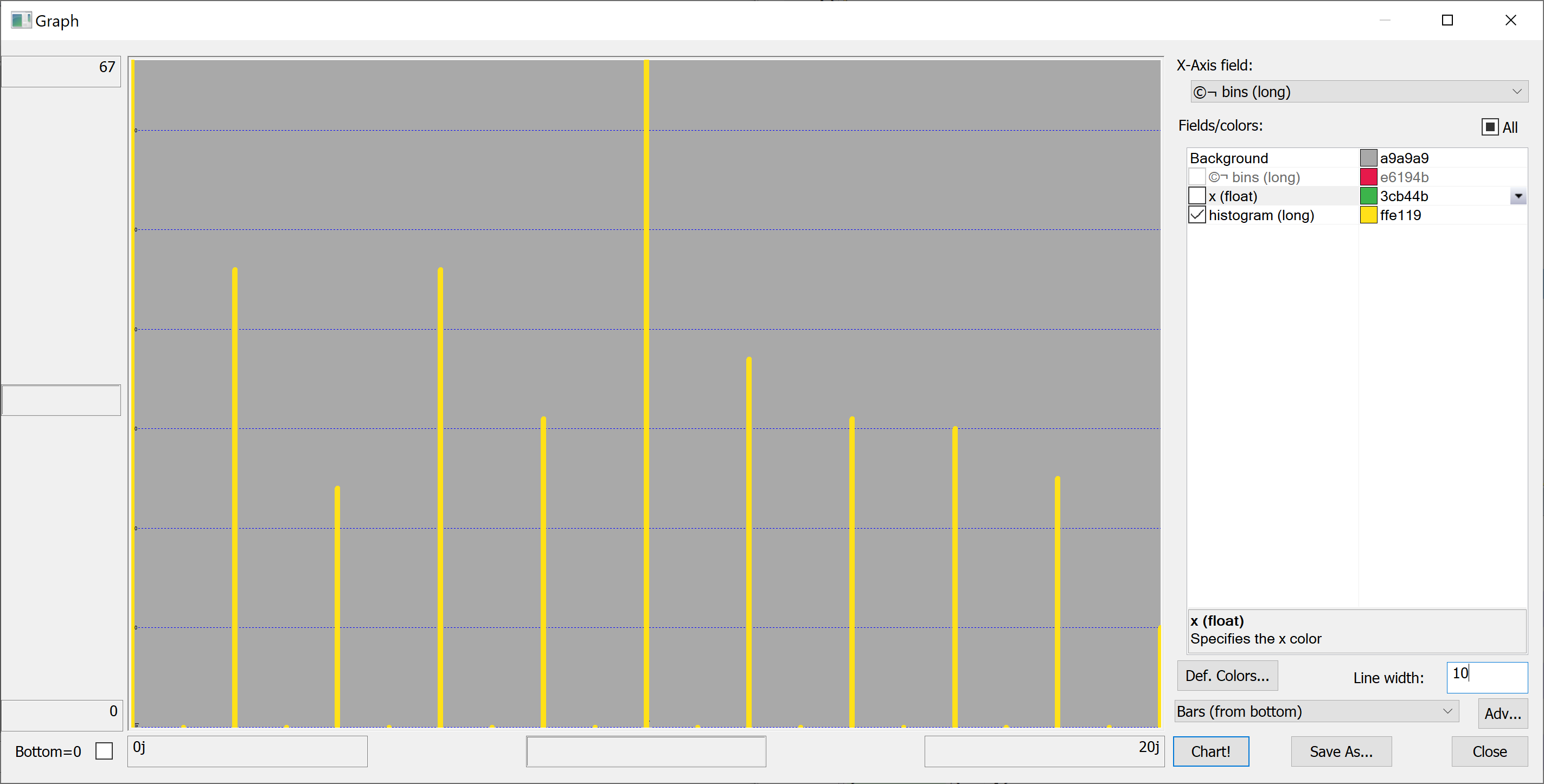
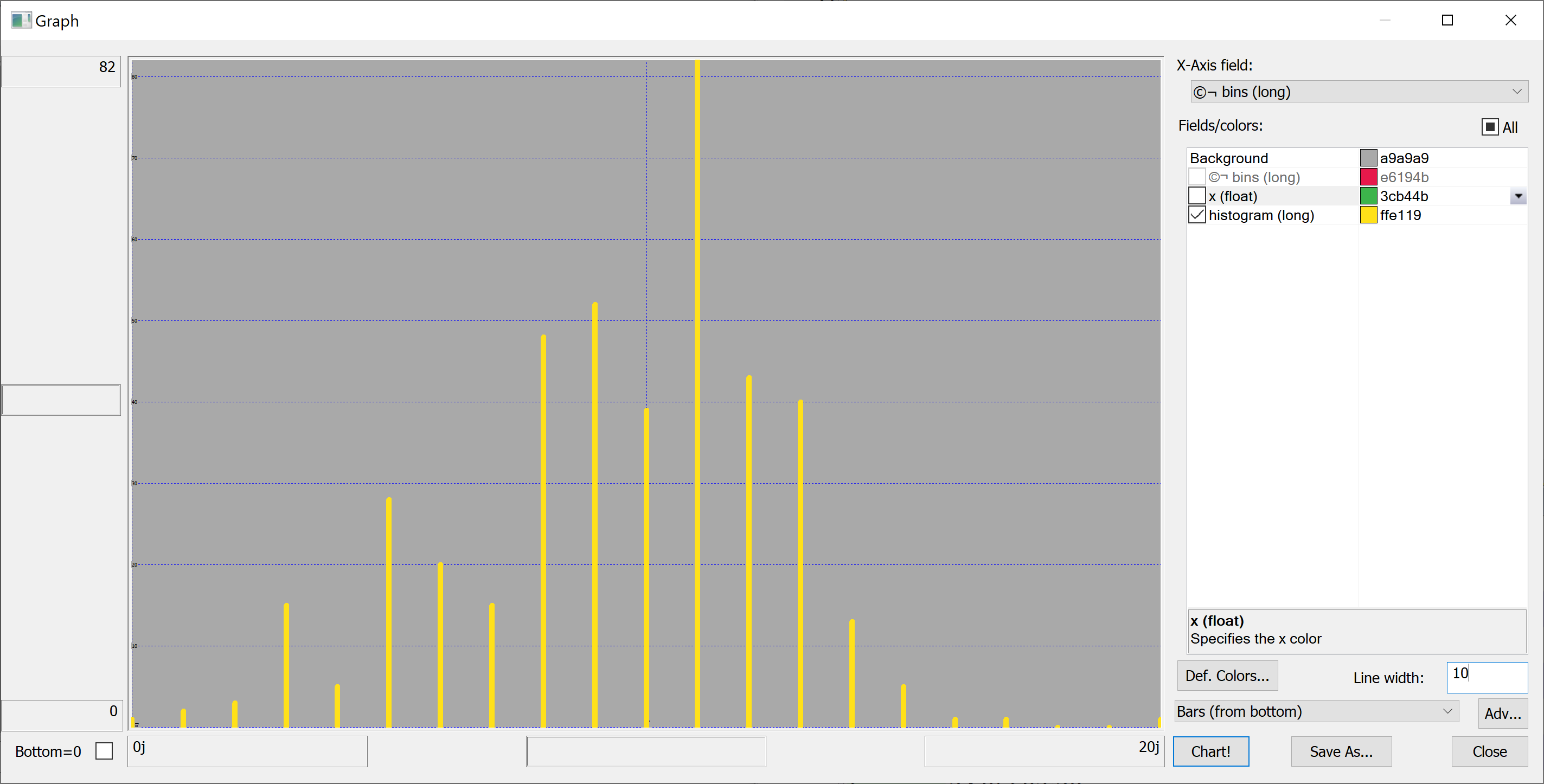
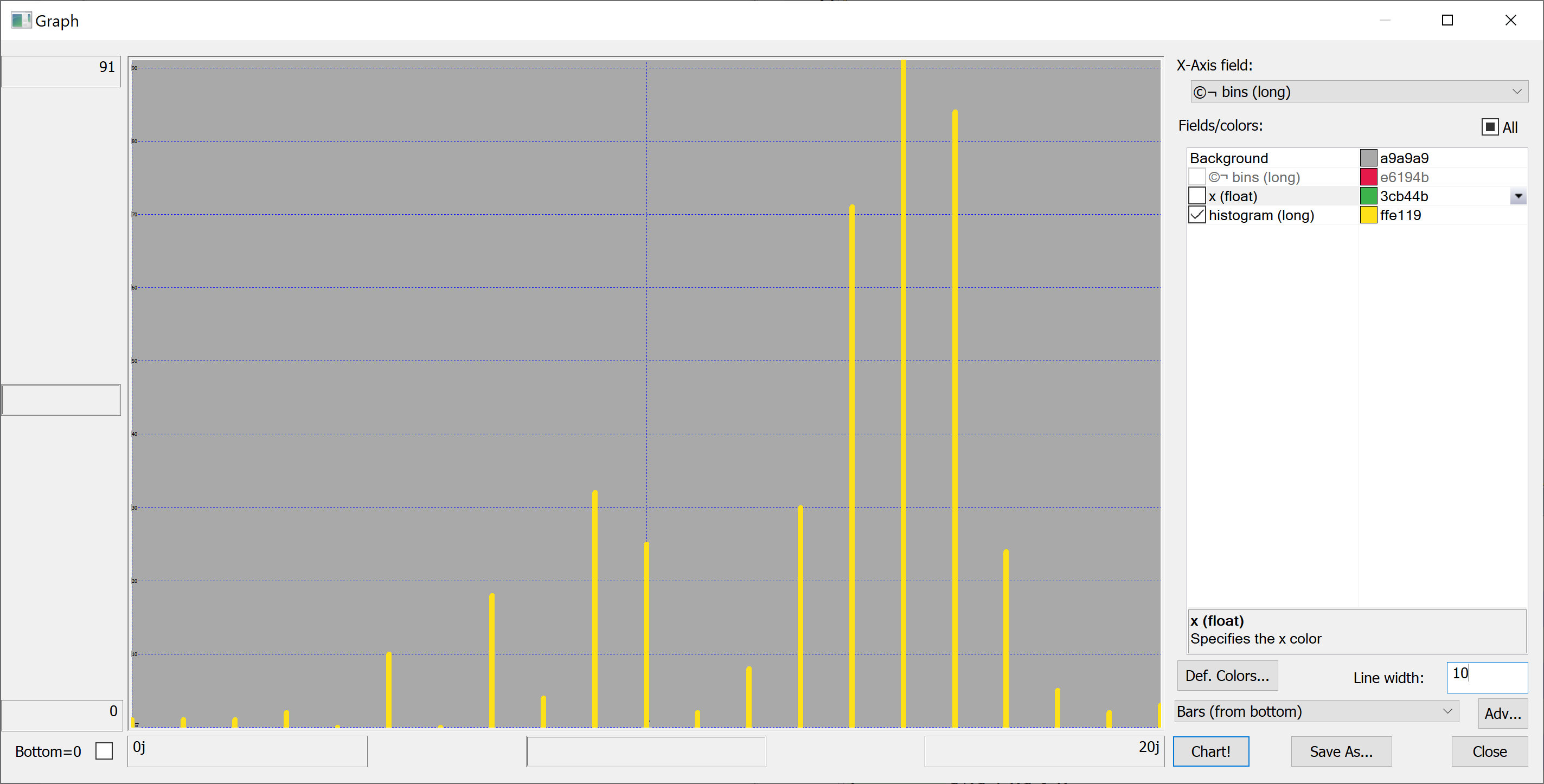
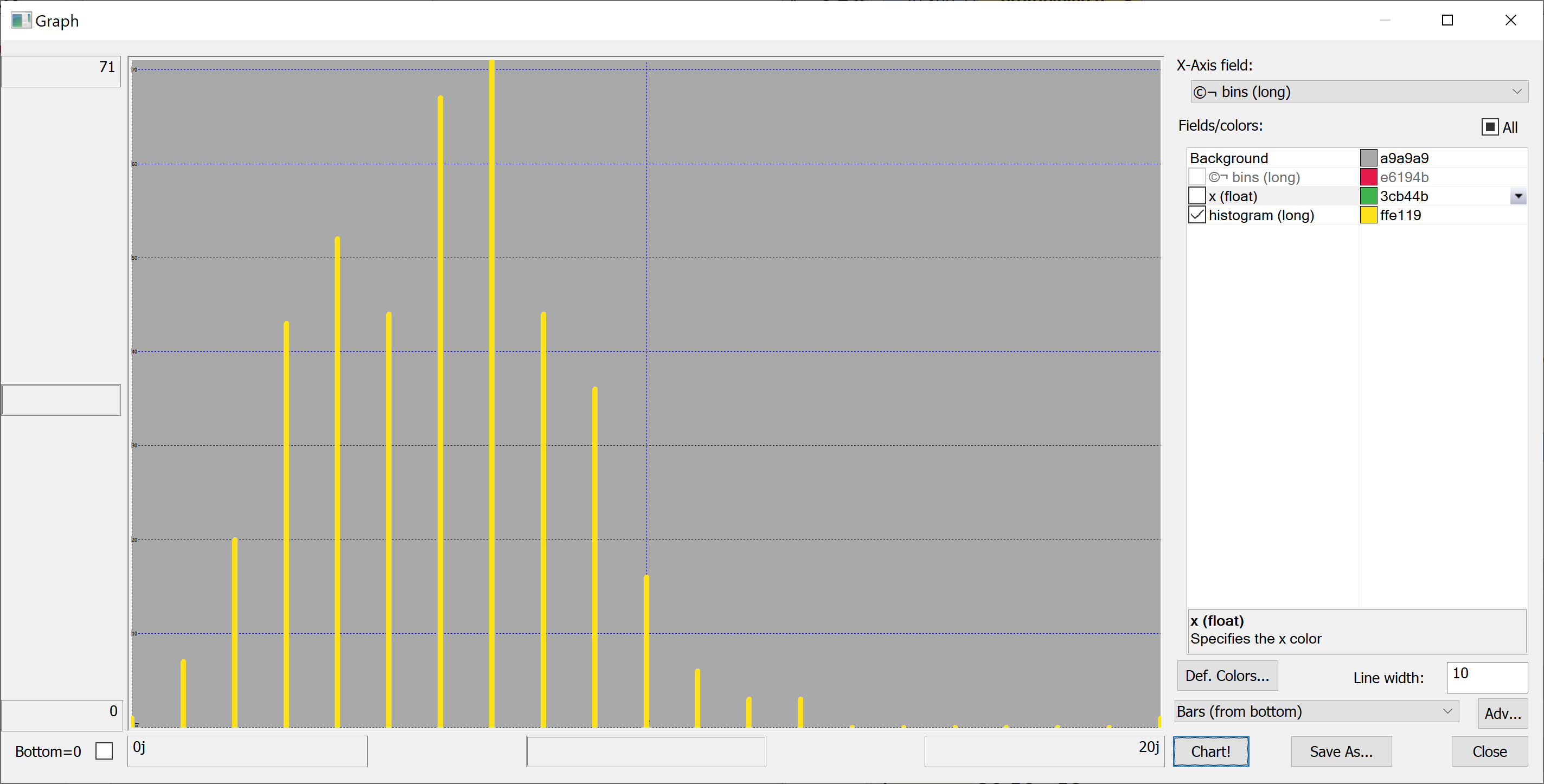
Equipped with this code, we can plot the histograms:

getHistogram[t[`transaction_date];histBin[20]]

getHistogram[t[`house_age];histBin[20]]

getHistogram[t[`distance_to_nearest_mrt];histBin[20]]

getHistogram[`float$t[`number_of_convenience_stores];histBin[20]]

getHistogram[t[`latitude];histBin[20]]

getHistogram[t[`longitude];histBin[20]]

getHistogram[t[`house_price_per_unit_area];histBin[20]]

A map

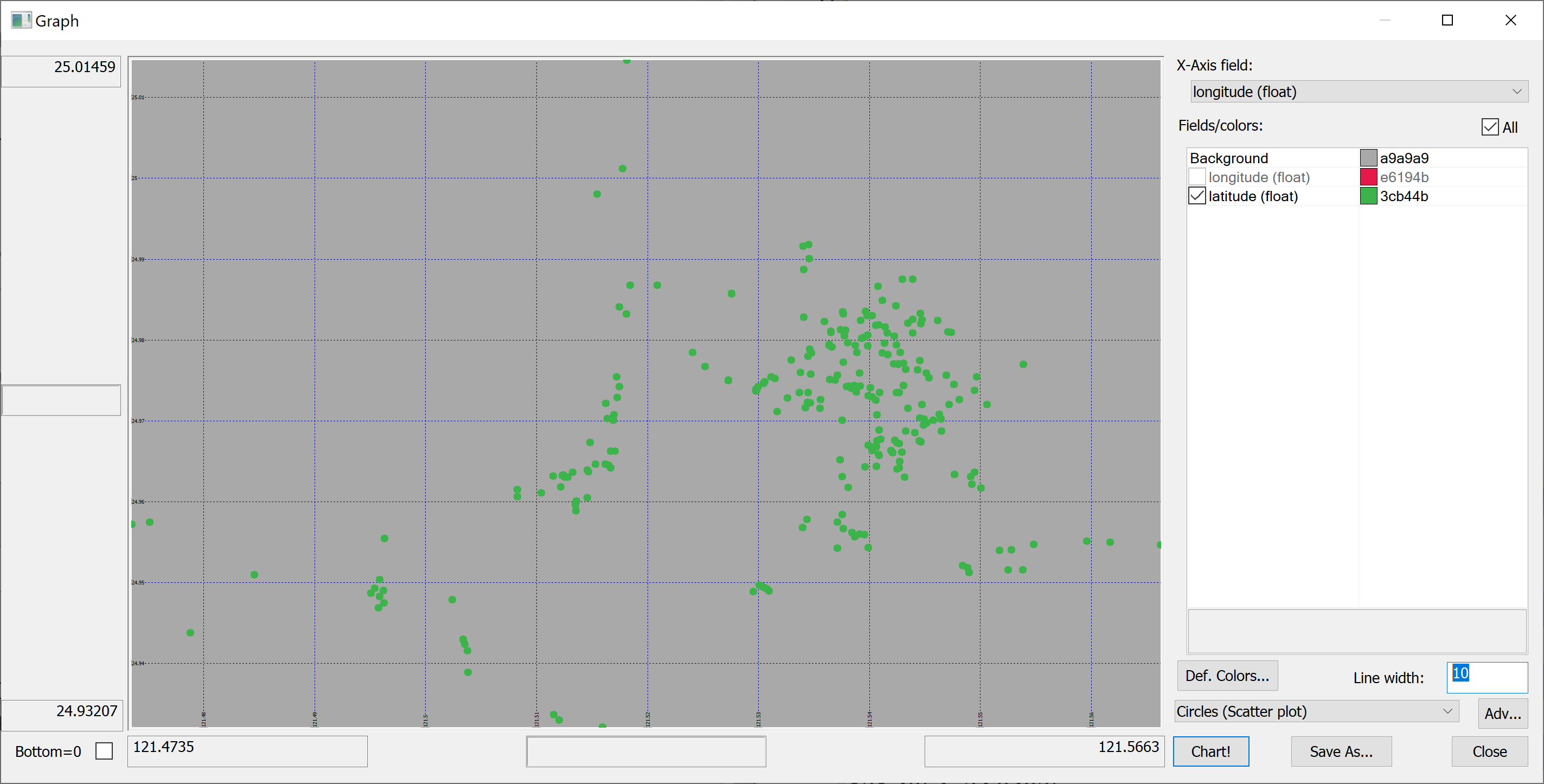
Since we have columns containing the longitude and latitude of each property, we can produce a map of all properties in the data set:

select longitude,latitude from t

Scatter plots

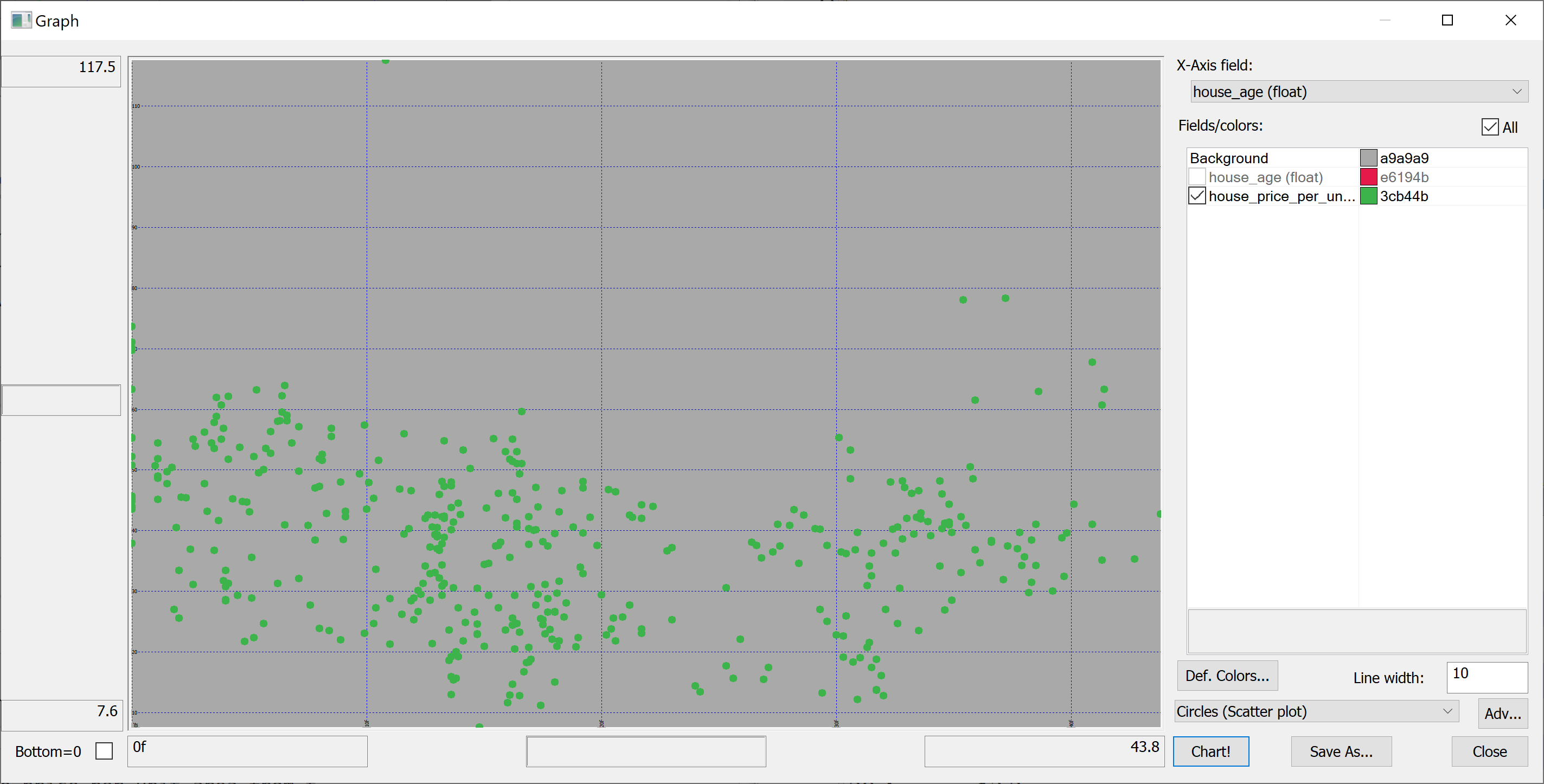
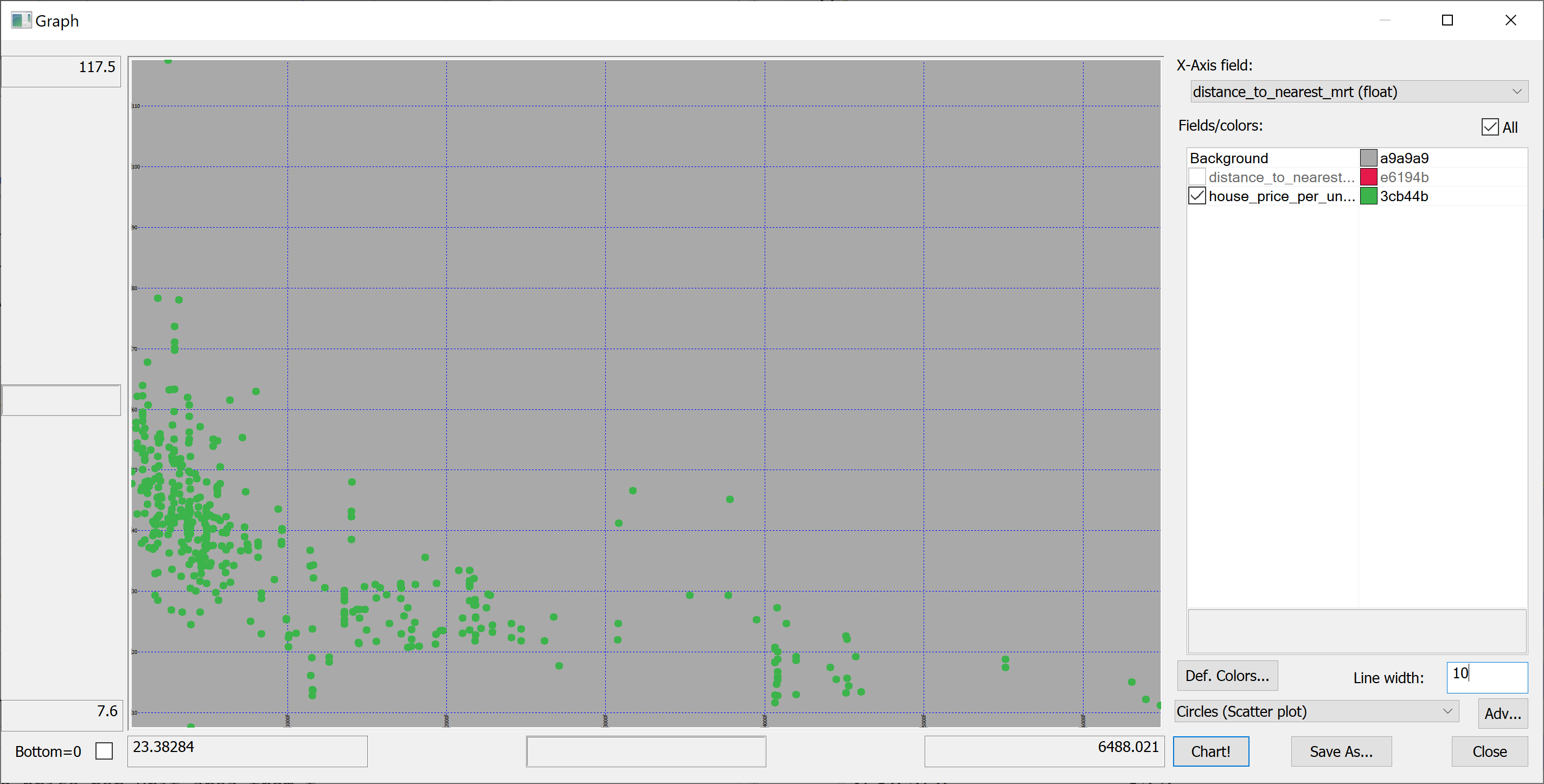
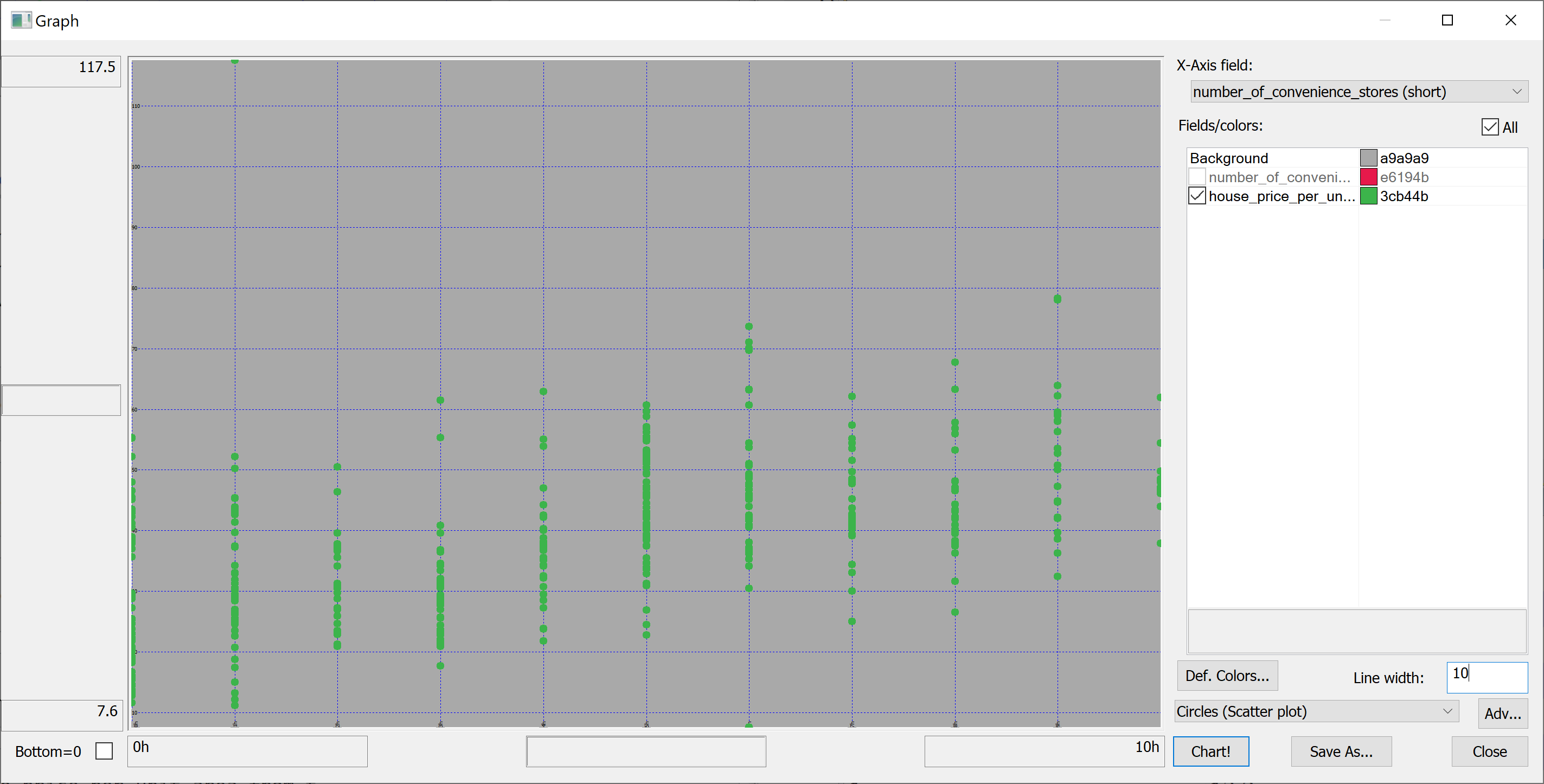
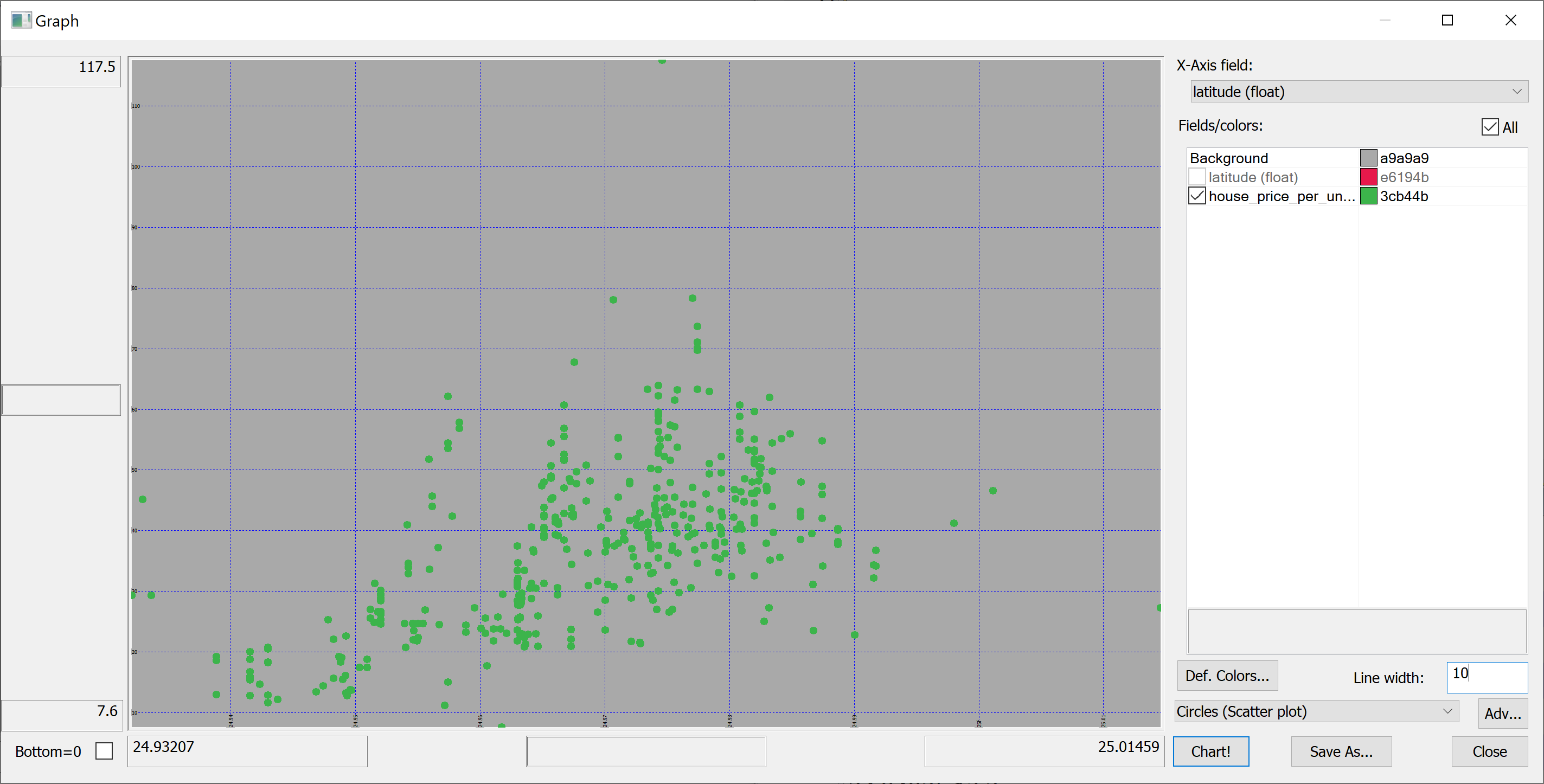
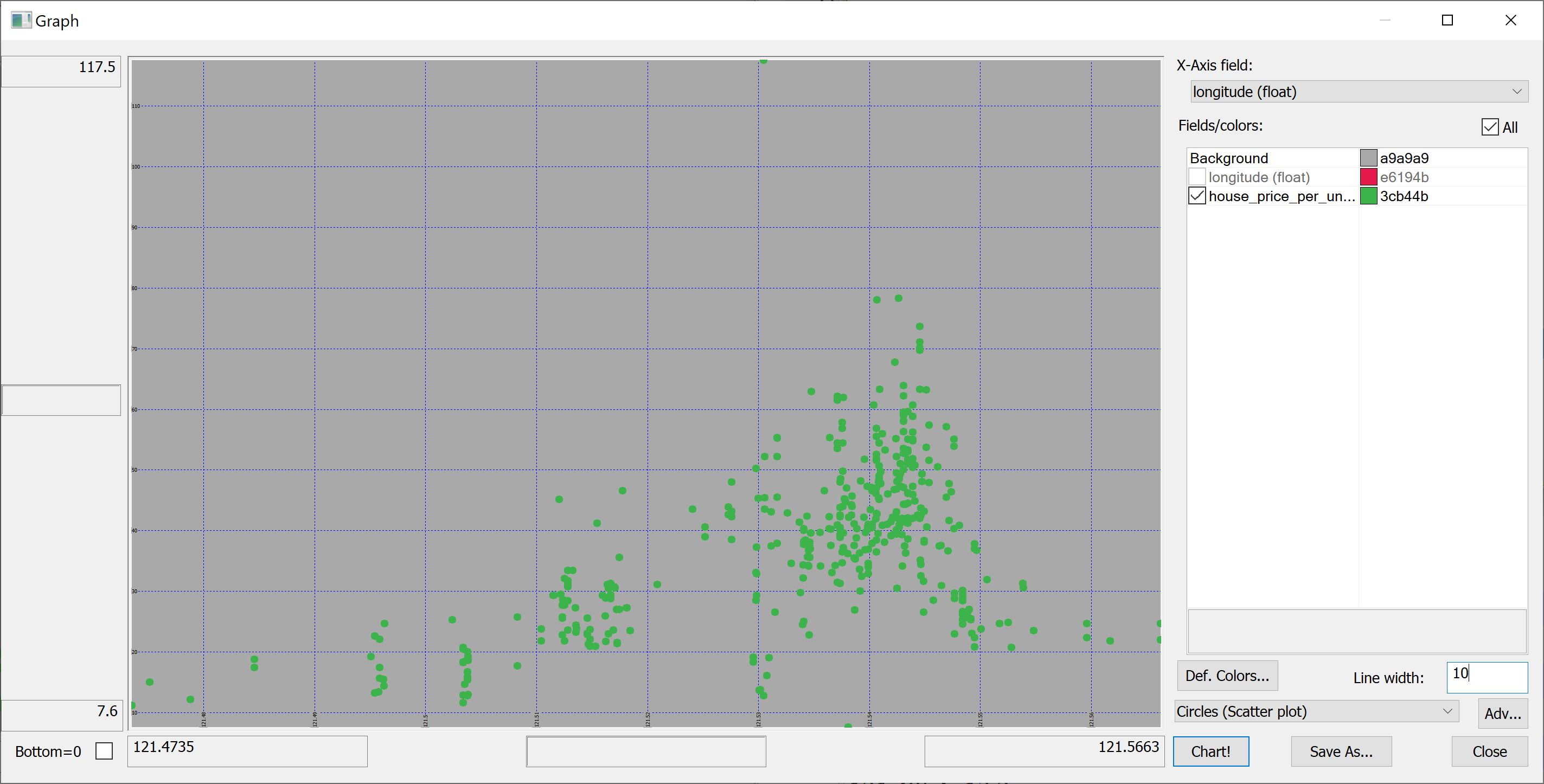
We are interested in predicting the house_price_per_unit_area using the various features present in our data set. Before we apply a machine learning algorithm, it is prudent to produce some scatter plots. The scatter plots could indicate whether each feature individually could help explain the house_price_per_unit_area.

select house_age,house_price_per_unit_area from t

select distance_to_nearest_mrt,house_price_per_unit_area from t

select number_of_convenience_stores,house_price_per_unit_area from t

select latitude,house_price_per_unit_area from t

select longitude,house_price_per_unit_area from t

Splitting the data

We are going to introduce some pseudorandomness, so it's a good idea to fix the seed to ensure reproducibility.

This can be done using the \S system command:

\S 42

We can now pseudorandomly shuffle the data:

n:count t;
t:neg[n]?t;

Let us use half of the data set as the training set and the other half as the test set:

n_train:n div 2;
n_test:n-n_train;

t_train:n_train#t;
t_test:neg[n_test]#t;

t_train and t_test are tables; we need matrices:

x_train:flip`float$t_train[-1_1_cols t_train];
y_train:raze t_train[-1#cols t_train];

x_test:flip`float$t_test[-1_1_cols t_test];
y_test:raze t_test[-1#cols t_test];

Linear regression using OLS

Suppose the data consists of $n$ observations $\{\mathbf {x} _{i},y_{i}\}_{i=1}^{n}$. Each observation $i$ includes a scalar response $y_{i}$ and a column vector $\mathbf {x} _{i}$ of $p$ regressors, i.e.

$\mathbf {x} _{i}={\begin{pmatrix}x_{i1}\\x_{i2}\\\vdots \\x_{ip}\end{pmatrix}}.$

In general, $n>p$. In a linear regression model, the response variable $y_{i}$ is a linear function of the regressors:

$y_{i}=\beta _{1}x_{i1}+\beta _{2}x_{i2}+\ldots +\beta _{p}x_{ip}+\epsilon _{i},$

or in vector form,

$y_{i}=\mathbf {x} _{i}^{\intercal }\mathbf {\beta } +\epsilon _{i},$

where $\mathbf {x} _{i}$, as introduced previously, is a column vector of the $i$th observation of all the explanatory variables; $\mathbf {\beta }$ is a $p\times 1$ vector of unknown parameters; and the scalar $\epsilon _{i}$ represents unobserved random variables (errors) of the $i$th observation. $\epsilon _{i}$ accounts for the influences upon the responses $y_{i}$ from sources other than the regressors $\mathbf {x} _{i}$. This model can also be written in matrix notation as

$\mathbf {y} =\mathbf {X} \mathbf {\beta } +\mathbf {\epsilon } ,$

where $\mathbf {y}$ and $\mathbf {\epsilon }$ are $n\times 1$ vectors of the response variables and the errors of the $n$ observations, and $\mathbf {X}$ is an $n\times p$ matrix of regressors, also sometimes called the design matrix, whose row $i$ is $\mathbf {x} _{i}^{\intercal }$ and contains the $i$th observations of all the explanatory variables.

How do we find the coefficients $\mathbf {\beta }$?

Consider the overdetermined system

$\mathbf {X} \mathbf {\beta } =\mathbf {y} .$

Such a system usually has no exact solution, so the goal is instead to find the coefficient $\mathbf {\beta }$ which fit the equations "best", in the sense of solving the quadratic minimization problem

${\hat {\mathbf {\beta } }}={\text{argmin}}_{\mathbf {\beta } }\|\mathbf {y} -\mathbf {X} \mathbf {\beta } \|^{2}.$

This minimization problem has a unique solution, provided that the $p$ columns of the matrix $X$ are linearly independent:

${\hat {\mathbf {\beta } }}=(\mathbf {X} ^{\intercal }\mathbf {X} )^{-1}\mathbf {X} ^{\intercal }\mathbf {y} .$